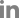1. 서 론
해상풍은 바다의 날씨를 결정하는 필수적인 기상요소일 뿐 아니라 해양과 대기의 상호작용에 직접 관여하기 때문에 다양한 해양모델의 중요한 입력자료로 사용되고 있다. 특히, 해상풍은 파랑과 해일 등 해양에서 발생하는 위험기상을 예측하거나 해상의 풍력자원을 추정하는 데에도 널리 사용된다. 우리나라는 신재생에너지 중 풍력을 핵심 에너지원으로 육성하기 위하여 그 비중을 2.2%에서 18.2%까지 증가시킬 계획을 갖고 있다(MTIE, 2014). 특히, 최근에는 소음 문제, 부지확보, 대규모 조성, 풍황 등에서 육상풍력보다 효율이 좋은 해상풍력에 대한 활용이 증대되고 있다.
해상풍력단지의 건설은 막대한 비용이 발생하므로 건설에 앞서 조성 지역에 대한 실제 풍속, 풍향 자료의 수집과 분석이 필요하며 해상에 설치된 풍력발전기의 위치에 따라 에너지의 효율이 달라지기 때문에 경제성 분석 또한 필요로 한다(Kyong et al., 2003; Min et al., 2014; Kim and Kang, 2017). 해상풍력단지의 경우 해상풍 뿐만 아니라 해수면의 변동, 파에너지 영향 등 설치 후 운영기간 동안에 발생 가능한 다양한 해양환경을 견뎌야 하기 때문에 극한 상황의 자료가 포함된 정확한 해상풍 자료가 요구된다(Yoon et al., 2014; Cho and Lee, 2016; Part et al., 2018). 그러나 풍력자원 추정 및 극치풍속 추정 등에 있어서 필수적으로 사용되는 극한 상황의 해상풍 자료를 얻는 것은 현실적으로 어려움이 있다. 해상은 육상과는 달리 관측이 제한적이기 때문이다. 실제로 기상청에서 운영되고 있는 해양기상 부이의 숫자는 육상관측 지점에 비해 매우 적어 원하는 위치에서의 관측된 해상풍 자료를 얻는 것은 매우 어렵다.
직접 관측의 이러한 한계를 극복하기 위해 최근에는 부이 관측자료 대신 QuikSCAT과 같은 위성자료로부터 얻은 해상풍이 해상풍력 자원평가와 극값 추정 등에 많이 사용되고 있다(Kyong et al., 2003; Jang et al., 2009). 그러나 위성기반 해상풍 자료도 해안에서 가까운 지역에서 자료의 획득이 어려울 뿐 아니라 설계된 풍속의 관측범위가 태풍 시기의 극한 풍속을 관측하는 데에는 한계가 있다(Ebuchi et al., 2002; Jeong et al., 2008; Son et al., 2020). 또한 해상풍을 관측하는 극궤도위성은 그 특성상 일정 경로만을 관측하기 때문에 시간 및 공간적으로 연속적인 관측자료를 얻는 데 제한이 있다.
우리나라에서 극한 풍속은 태풍 시기에 때 많이 발생한다. 따라서 태풍 시기에 정확한 해상풍 자료는 극치분석을 위해 필수적인 자료이다. 그러나, 태풍 시기에 해상 부이로 부터 해상풍 자료를 얻는 것은 더욱 어렵다. 왜냐하면 평소에 잘 관측하던 해상 부이도 태풍 시기에는 결측되는 경우가 많기 때문이다. 위성자료도 앞서 언급한 바와 같이 태풍 시기의 강한 바람에서는 오차가 커진다. 태풍 시기의 이러한 관측의 한계를 극복하기 위하여 많은 연구자들은 Holland 경험모델을 사용하여 태풍 바람장을 추정한다(Holland, 1980; Willoughby and Rahn, 2004). 그러나 Holland 경험모델은 태풍의 원형 및 대칭성을 가정하고 만들어지기 때문에 태풍이 외해에서 강한 강도를 유지할 때는 잘 맞지만 북상하면서 강도가 약해지고 상륙 시에 육지에 영향을 받아 원형 구조가 깨어져 비대칭적 형태로 바뀌게 되면 모의된 바람장은 부정확해지게 된다. 또한 Holland 모델은 그 특성상 태풍의 외곽 바람을 모의하지 못하고 비 태풍 시기에 해상풍을 추정하지 못하는 단점이 있다. 겨울철에 평균적으로 바람이 더 강한 우리나라 근해의 해상풍의 특성을 고려하면 비 태풍 시기의 해상풍 자료도 극치분석에 포함되어야 한다. 실제로 우리나라 근해 풍랑특보(풍랑주의보 및 경보 포함) 일수를 보면, 12월에 가장 많고 1월과 3~4월에도 높은 빈도를 보여 비 태풍 시기에 더 강한 바람이 불고 있음을 알 수 있다(Seol, 2017). 따라서 태풍 시기 동안에 태풍 중심 부근 바람장만 모의할 수 있는 Holland 모델도 극치분석에 활용하는 데에는 한계가 있다.
시⋅공간적으로 해상도가 비교적 높고 태풍 시기 뿐만 아니라 비 태풍 시기의 해상풍 자료를 얻을 수 있는 방법은 수치모델을 통해 생산된 재분석장 자료를 활용하는 방법이 있다. 일반적으로 3-6 시간 간격으로 25-100km 공간해상도로 제공되는 재분석 바람장은 특히 관측자료가 부족한 해상풍 분석에 널리 사용될 수 있다. 그러나 재분석장 바람도 태풍 중심의 강한 바람을 현실적으로 모의하지 못해, 해상풍의 극치분석에 활용하는 데에는 그동안 한계가 있었다.
본 연구에서는 재분석 바람장 속에 모의된 태풍에 대해 크기 및 강도를 보정하고 중심위치를 조정(vortex relocation)하는 보거싱(Bogussing) 기법이 적용된 미국 국립환경예보센터(National Centers for Environmental Prediction, NCEP)의 최신 Global Forecast System (GFS) 재분석장(NCEP, 2018)을 사용하여 한반도 근해에서 해상풍의 정확도를 평가하고 극치분석을 실시하였다. 아직까지 보거싱이 적용된 GFS 재분석장은 비교적 짧은 기간(10년) 동안에만 자료를 얻을 수 있어 이를 극복하기 위하여 Peak-Over-Threshold(POT) 방법을 극치분석에 사용하였다. POT 방법은 특정 임계값 이상의 풍속을 모두 사용하여 자료의 기간이 짧은 경우에 적합한 극치분석 방법이며, 일반화된 파레토 분포(Generalized Pareto Distribution, GPD) 방법을 사용하여 구현된다(Pareto, 1897).
2장에서는 본 연구에 사용된 자료와 분석방법(오차분석, 고도에 따른 해상풍 변환, 극치분석)에 대해 설명한다. 3장에서는 기상청 해양기상 부이와 비교를 통하여 GFS 재분석 바람장의 정확도를 태풍 시기와 비 태풍 시기로 나누어 평가한다. 4장에서는 GFS 재분석 바람장을 이용하여 한반도 근해의 극치 풍속을 추정하고, 지역별 및 시기별로 우리나라에서 극값을 유발하는 강한 풍속에 대해 그 분포 특징 및 원인에 대해 분석한다.
2. 자료 및 분석방법
본 연구에서 사용된 NCEP GFS 재분석 자료는 대기모델, 해양모델, 육지/토양 모델, 해빙모델이 결합되어 온도, 바람, 강수량에서부터 토양 수분과 대기 오존 농도 등 수십 가지의 대기 및 육지 토양 변수를 제공하고 있다. GFS 모델은 하루에 4번(00, 06, 12, 18 UTC) 자료를 제공하며 공간해상도는 0.5° x 0.5°, 수직해상도는 64개 층으로 구성되어 있다. 분석에 사용된 자료의 기간은 2009년부터 2018년까지 총 10년이다. GFS 재분석장의 장점은 태풍의 강도, 크기, 위치를 보정하기 위해 중심위치 조정 기법이 적용된 보거싱 방법이 사용된 점이다. 보거싱 기법은 모조 태풍의 위치, 크기, 강도를 실제 관측자료를 기반으로 만들어 재분석장에 삽입하는 방법이다(NCEP, 2018). GFS 재분석장은 2010년 7월 말부터 새롭게 적용된 PBL scheme을 통해서 그 동안 문제가 되었던 동태평양과 대서양에 성층구름의 과소평가와 grid 스케일에서 과도한 강수량의 문제를 개선하여 그 성능이 크게 개선된 것으로 알려져 있다(Han and Pan, 2011).
한반도 근해에서 GFS 재분석장의 정확도는 기상청 해양기상 부이와 비교를 통해 평가되었다(Fig. 1). GFS 재분석장의 격자점과 해양기상 부이의 관측 위치는 일치하지 않기 때문에 Shepard(1968)에 따른 역거리 가중법(Inverse Distance Weighting, IDW)을 사용하여 GFS 값은 부이 위치로 변환하여 사용하였다(Eq. (1) 참고). 역거리 가중법은 일종의 공간내삽 방법으로 주위 인접한 값에 더 가중치를 두어 특정 지점의 값을 예측하는 방법이다(Longley et al., 2005; Burrough et al., 2013).
여기서 X는 보간할 지점이고, Xi는 보간에 사용될 인접한 지점의 4개 GFS 격자값이다. wi(X)는 X의 값을 결정할 때 사용한 Xi의 거리에 따른 가중치이다. 즉, 거리가 가까울수록 wi(X)값이 크게 되어 더 큰 가중치가 적용된다. d는 X로부터 Xi까지의 거리이다. p는 거리감쇠계수로 양의 실수값을 사용한다(Shin and Kim, 2015).
GFS 재분석장의 풍속은 고도 10m의 자료이지만 해양기상 부이는 3.6~4.0m 고도에 풍속계가 설치되어 있어 두 고도를 맞추어 바람을 비교해야 한다. 해양기상 부이에서 관측된 풍속을 GFS의 10m 해상풍 고도로 바꾸는 방법은 선행연구에서 사용된 해상풍 변환식(Eq. (2) 참고)을 사용하였다(De Rooy and Kok, 2004; Oh and Ha, 2005; Jeong et al., 2008; Park et al, 2018).
이 식은 대기의 안정도를 중립상태로 가정하여 안정도 함수를 0으로 적용한 것이며, U10은 10m 고도의 해상풍을, UH는 관측 고도 H에서의 해상풍을, 그리고 Z0는 풍속이 0이 되는 고도의 거칠기 길이를 의미한다(Oh and Ha, 2005). 본 연구에서 사용된 거칠기 길이는 해양기상 부이가 외해 보다는 연안에 근접해 있기 때문에 Stull(1988)이 제시한 연안의 거칠기 길이인 10-3 m을 사용하였다.
GFS 정확도 분석은 2009년부터 2018년까지 10년 기간에 대해 실시되었지만 해양기상 부이마다 자료 기간에 차이가 있어, 공평한 비교를 위하여 모든 부이에서 자료가 존재하는 2016-2018년에 대해서는 추가 분석을 실시하였다. GFS 분석장의 정확도는 평균제곱근편차(Root Mean Square Error, RMSE), 편차(Bias), 상관계수(Correlation, r)를 사용하였다(Eqs. (3), (4) and (5) 참고).
여기서 M은 모델값, O는 관측값 그리고 N은 자료의 개수이다.
본 연구에서 한반도 근해의 극치 풍속을 추정하기 위해서 사용된 방법은 일반화된 파레토 분포(GPD, Eq. (6) 참고)이다(Pareto, 1897; Pickands, 1975). 이 방법은 주어진 임계치를 넘어가는 자료를 모두 사용하여 극치분석을 수행하기 때문에 자료의 기간이 짧은 극치분석에 널리 이용된다(Davidson, 1984; Castill and Hadi, 1997; Castillo and Daoudib, 2008; Huh and Sohn, 2014). 극치모형의 매개변수 추정은 최우도법(Method of Maximum Likelihood)을 사용하였다.
GPD 모델의 파라미터는 규모매개변수 σ, 형태매개변수 k, 그리고 임계값 θ로 구성되어 있으며, 자료 분포의 꼬리 부분을 모형화하여 사용된다. GPD 모델은 자료의 독립성이 요구되기 때문에 θ보다 큰 값이 연속적으로 선택되지 않도록 선택된 자료의 ±12시간 미만의 자료는 사용하지 않았다. 재현기간(T, Return period)의 풍속은 확률 P의 역수로 나타낼 수 있다(Eq. (7) 참고).
여기서 n은 임계값 θ 이상의 선택된 관측자료들의 개수이며, N은 연수에 따른 선택된 관측자료의 개수를 의미한다.
3. GFS 재분석 바람장 정확도 분석
2009년부터 2018년까지 총 10년간 부이자료와 재분석장의 풍속을 비교하였다. 먼저 부이 관측자료가 있는 모든 시기(period 1)에 비교를 실시하였다. 여기서 한가지 유의할 점은 2009년부터 2015까지 기간에는 자료가 없는 부이들이 존재한다는 것이다. 따라서 부이별 오차를 상대적으로 비교하기 위해서 모든 부이자료가 공통적으로 존재하는 2016년부터 2018년에 기간(period 2)에 대해 정확도 평가를 따로 실시하였다. 또한 태풍 시기의 재분석 바람장의 정확도를 조사하기 위하여 2009년부터 2018년까지 한반도에 영향을 미친 태풍 시기에 대해 한정하여 추가적인 분석을 실시하였다.
3.1 전체 기간의 정확도
전체 기간(Period 1)에 대한 통계분석 결과, 전체적으로 Bias는 -0.33m/s, RMSE는 1.95m/s, 상관도는 0.86으로 나타나, 재분석 바람장이 한반도 근해의 해상풍을 비교적 정확하게 모의하는 것으로 나타났다. Bias (GFS-부이)가 음의 값을 나타내는 것은 전체적으로 GFS가 해상풍을 과소모의 하고 있음을 의미한다. 이러한 편차는 GFS 모델 자체의 오차와 가장 큰 관련이 있겠지만 그 외 해양기상 부이와 모델 결과를 비교하기 위해 사용된 역거리 가중법에서 부이를 둘러싼 4개의 GFS 격자점을 평균하는 과정에서도 발생할 수 있다. 즉, 육지와 인접한 해양기상 부이에서 역거리 가중법을 사용하게 되면 모델이 격자점에서 풍속을 정확히 모의하였더라도 풍속이 상대적으로 낮은 육지의 GFS 격자점이 포함되어 실제의 바람보다 약한 바람이 나타날 수 있다. 예를 들면, 음의 편차가 큰(Bias<-0.5m/s), 즉 풍속을 과소 모의하는 경향이 큰 거제도와 포항 등은 역거리 가중법에 사용된 GFS의 격자점에 육상(또는 육상 근처)의 지점이 많이 포함된 것이 영향을 미쳤을 가능성이 있다(Fig. 1). 반대로 칠발도와 울릉도와 같이 바람이 강한 외해의 격자점이 더 포함된 지점은 평균하는 과정에서 오히려 풍속을 과대 모의할 수 있다.
해역별로 보면 서해와 남해는 비교적 낮은 편차(-0.5m/s<Bias<0.5m/s)를 보인 지점이 많이 위치해 있었으며, 그에 반해 동해와 제주 남부는 과소모의 경향이 큰(Bias<-0.5m/s) 지점이 많았다. RMSE의 경우, 오차가 비교적 큰 지역(RMSE>2m/s)은 거제도, 포항, 마라도, 서귀포, 울산, 울진 등으로 나타났으며, 이들 지점은 신안을 제외하면 모두 편차가 큰(Bias>|0.5m/s|) 지역이었다. 상관도의 경우 모든 지점에서 0.8 이상의 높은 상관도를 보였으며 지역적으로 뚜렷한 차이는 보이지 않았다.
3.2 태풍 시기 정확도
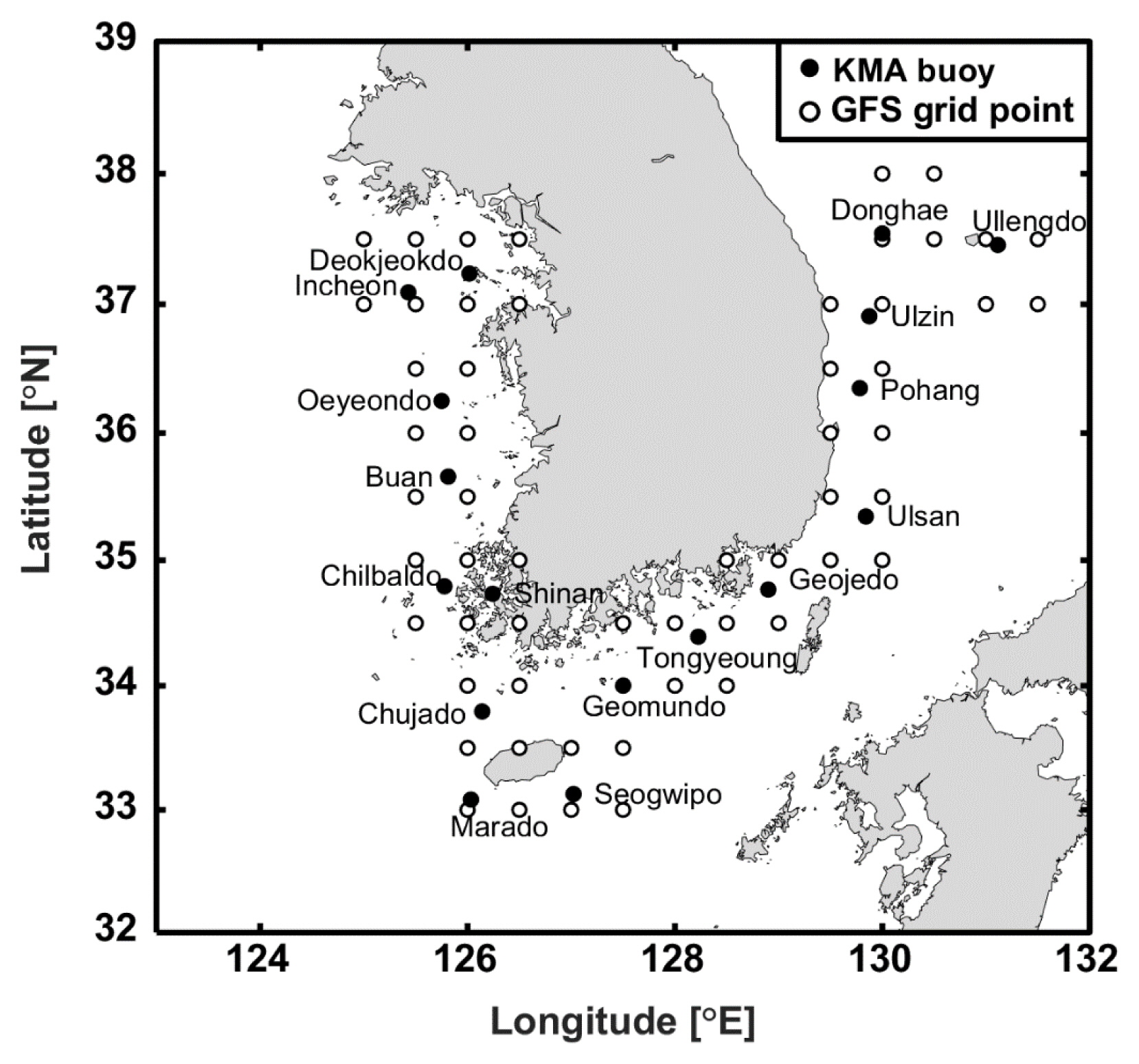
극치분석에서는 전체 기간의 정확도보다 강한 풍속이 발생했을 때 정확도가 더 중요하다. 이에 본 연구에서는 강한 풍속이 발생하는 태풍 시기에 해상풍의 정확도를 파악하기 위해서 2009년에서 2018년까지 한반도에 영향을 미친 35개의 태풍 시기에 대해 GFS 재분석자료와 기상부이 자료를 비교하였다. 한반도 영향 태풍의 목록은 Table 2에 그리고 태풍의 이동경로는 Fig. 2에 나타내었다.
태풍 시기의 GFS 바람장의 정확도를 앞선 전체 기간(Period1, 2)의 결과와 비교해 보면, Bias(-0.14m/s)는 줄어들었지만 RMSE(2.22m/s)는 더 커졌다. 상관도(r =0.85)도 유의하지는 않지만 약간 작은 값을 보였다. 이렇게 태풍 시기에 오차가 일부 커진 이유는 태풍 시기의 강한 풍속으로 인해 평균 풍속이 증가한 것과 관련성이 있다. 일반적으로 평균 값이 커지면 오차가 증가하는 경향이 있기 때문이다. 태풍 시기 GFS 바람장의 모의 성능을 시계열로 확인하기 위해 한반도를 통과한 2018년 19호 태풍 솔릭 시기에 대해 재분석장과 부이 자료를 비교하였다. 솔릭은 2018년 8월 22일에 제주도 부근 해상가지 접근하여 매우 느리게 북진하다가 23일 오후 목포 남서쪽 해상에서 급격하게 전향해 23일 23시경 목포 남쪽 20km 부근 육상에 상륙하였다. 솔릭은 그 후 계속 북동진하여 25일 새벽 독도 북북동쪽 약 480km 부근에서 온대저기압으로 변질되었다. 솔릭시기에 GFS 바람장의 정확도는 17개 지점에서 8월 21일에서 26일까지 태풍이 통과한 기간에 대해서만 이루어졌다(Fig. 3). 그림에서 해양기상부이와 GFS의 값은 회색 실선과 검은색 점선으로 각각 표시되었으며 우측 상단에는 통계 결과가 제시되었다. 대부분의 부이에서 GFS 분석장은 관측자료와 매우 유사하게 태풍 시기에 변화하는 풍속을 잘 모의하고 있다. GFS 모델의 공간해상도가 약 50km 인 것을 감안하면, 태풍 솔 릭 시기의 0.85의 상관도, 2.22m/s 의 RMSE, 그리고 0.14m/s의 Bias는 태풍 시기에도 GFS 분석장이 풍속을 현실적으로 잘 모의하였음을 의미한다(Fig. 3(r)).
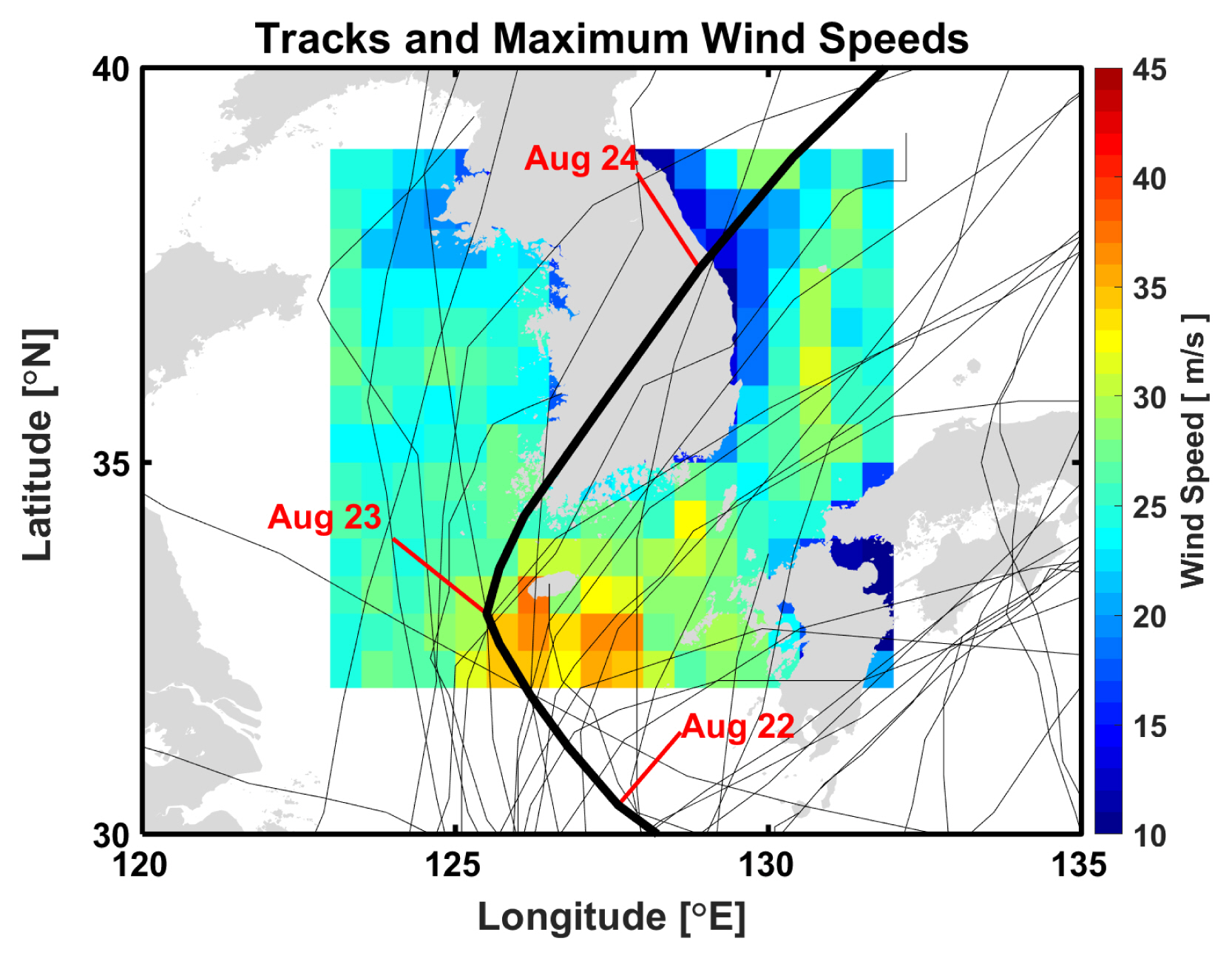
극치분석에서는 태풍에 대한 전체적인 모의 성능보다 최대풍속을 얼마나 잘 모의하느냐가 더 중요할 수 있다. Fig. 3에서 GFS의 최대풍속의 모의 성능을 보면, 포항, 신안, 추자도, 울산을 제외한(Fig. 3(g), (j), (k), (p)) 대부분의 지점에서 분석장의 최대풍속이 부이와 거의 일치하였다. 같은 방법으로 35개 태풍에 대해 모든 부이 지점에서 GFS 분석장의 풍속이 태풍 통과 기간 동안 최대값을 가질 때, 해양기상 부이와 모델결과를 비교해보면(Fig. 4), Bias는 1.08m/s, RMSE는 3.21m/s, 상관도는 0.79으로 나타난다. 이 결과는 앞선 태풍 시기 모든 자료를 이용한 결과보다는 오차가 크지만 다른 재분석장의 결과와 비교했을 때 태풍 시기의 최대풍속을 비교적 정확하게 모의하는 것으로 사료된다. 참고로 일반적인 재분석 바람장은 태풍 시기의 최대풍속을 매우 과소 모의하며, 심지어 20m/s 이상의 강한 바람은 거의 모의하지 못하는 것으로 알려져 있다. GFS 분석장에서 일부 지점의 최대풍속이 잘 모의되지 못한 이유 중 하나는 GFS 모델의 공간해상도가 낮아 지형변화가 큰 지역에서 실제 부이 위치와 모델의 격자점이 차이가 나기 때문으로 사료된다.
4. 한반도 극치 해상풍 추정
4.1 GPD 모델의 임계값 설정
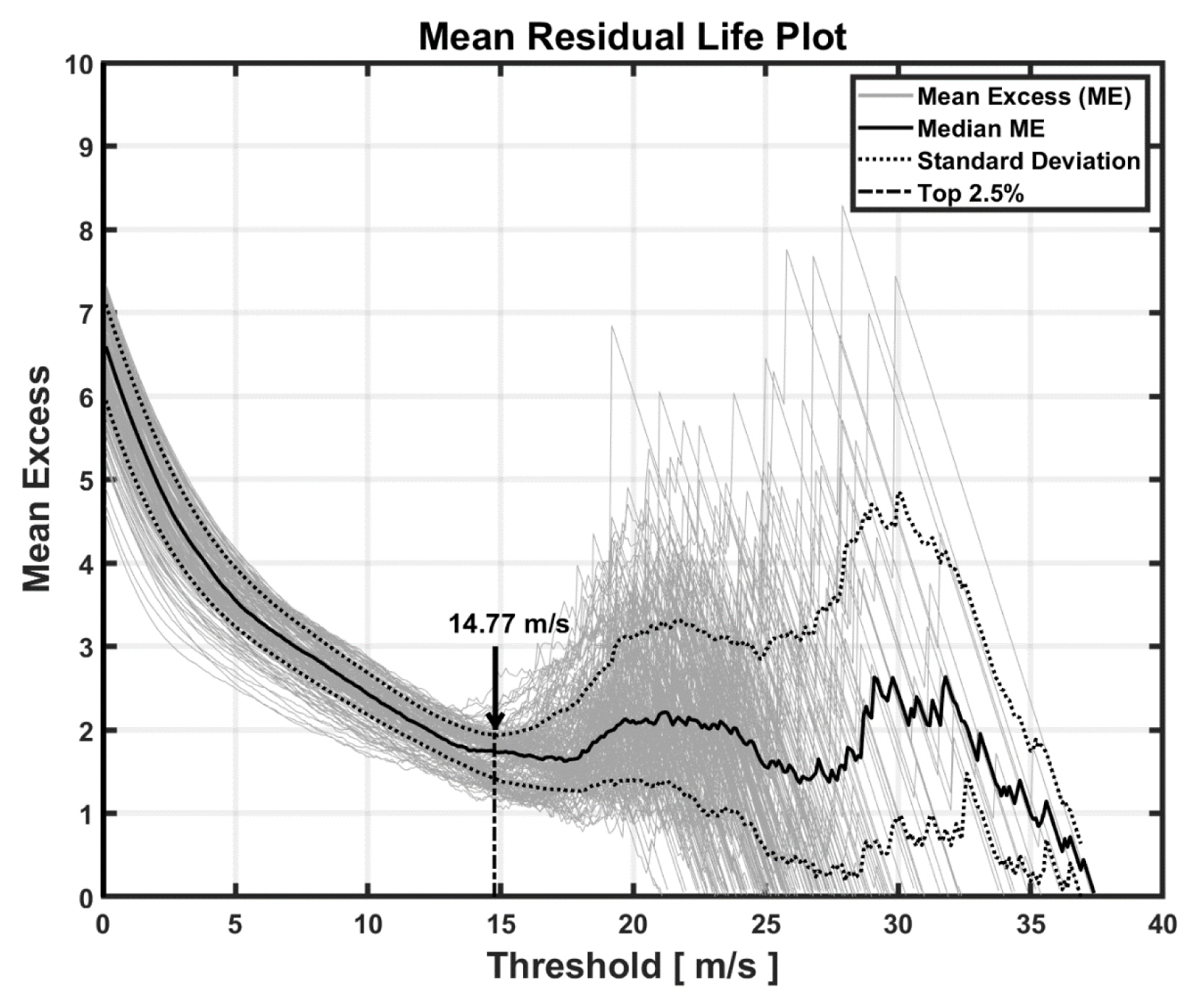
본 연구에서는 한반도 근해의 극치 해상풍을 추정하기 위해 POT 방법과 GPD 모델을 사용하였다. GPD 모델을 이용한 극치풍속 추정 방법은 설정한 임계값 이상의 독립된 모든 풍속이 사용되기 때문에 임계값 설정이 매우 중요하다. 일반적으로 GPD 모델의 임계값은 Coles et al.(2001)이 제시한 Mean Residual Life(MRL) plot를 사용하여 설정된다. Coles et al.(2001)에 따르면 적절한 임계값은 비선형적인 곡선 형태를 보이는 MRL plot에서 직선 구간으로 바뀔 때의 값으로 설정된다. 본 연구에서도 Coles et al.(2001)이 제시한 MRL plot을 사용하여 임계값을 추정하였다(Fig. 5). 여기서 모든 격자점의 MRL plot은 회색 실선으로 중앙값은 검은 실선으로 표시되었다. 그림에서 MRL plot이 직선 구간으로 나타나는 범위는 14~16m/s로 추정되어 이 범위 중에 적절한 임계값이 선택될 수 있다.
임계값을 이러한 방법으로 정하게 되면, 결국 앞에서 구한 14~16m/s로 범위에서 주관적으로 한 값을 결정할 수밖에 없다. 따라서 본 연구에서는 Jung et al.(2018)이 제시한 Generalized Extreme Value(GEV) 모델과 GPD 모델의 재현기간 풍속의 차이를 통해 객관적으로 GPD 모델의 임계값을 설정하는 방법을 이용하였다. 이 방법에 따르면 임계값은 상위 1~10%까지 설정한 GPD 모델의 재현기간 풍속과 GEV 재현기간 풍속을 비교하여(Fig. 6) 그 차이가 가장 작을 때로 결정된다(Eq. (8) 참고).
여기서 X T i G P D X T i G E V
4.2 GPD 모델을 이용한 재현기간 극치풍속 추정
본 연구에서는 앞서 설명한 방법으로 한반도 근해에서 재현기간 50년의 극치풍속을 구하고, 이를 서해, 동해, 그리고 제주도 남부해역으로 나누어 분석하였다(Fig. 7). 재현기간 50년의 극치풍속을 해역별로 비교해 보면, 제주도를 포함한 제주도 남부해역(C, 37~66m/s)에서 가장 높은 풍속을 보였고, 그 다음으로 동해(B, 24~36m/s), 서해(A, 23~27m/s) 순으로 나타났다. GPD 모델로부터 추정된 극치풍속의 공간적인 분포는 태풍 시기에 나타난 최대풍속 분포(Fig. 2)와 유사한 형태를 보인다. 이것은 우리나라 근해의 극치풍속 분포가 태풍에 의해 크게 영향을 받음을 시사한다. 그러나 앞에서 언급한 바와 같이 우리나라는 겨울철에 평균적으로 풍속이 강하고, 때때로 태풍 강도(17m/s) 이상의 강풍이 자주 발생한다. 실제로 앞서 구한 임계 풍속(14.77m/s) 이상의 강풍 출현확률을 해역별 및 월별로 살펴보면(Fig. 8), 모든 해역에서 12월에 가장 강풍 발생확률이 높고 6월에 가장 낮음을 알 수 있다. 이 결과는 2006~2013년까지 8년 동안 월평균 풍랑특보일이 6월이 가장 낮고 12월이 가장 높았다고 보고한 Kim and Kim(2014)의 결과와 일치한다.
11월에서 1월까지 겨울철의 강풍 발생 비율을 세 해역에서 비교하면, 서해에서 가장 높고 제주도 남쪽에서 가장 낮게 나타난다. 이것은 겨울철에 대륙에서 불어오는 북서풍이 서해와 동해에서 강하게 불기 때문이다. 제주도 남쪽 해역은 한반도에 태풍이 가장 많이 영향을 미치는 8월에 다른 두 해역에 비해 강풍의 출현확률이 거의 두 배 정도 크게 나타난다. 4월과 5월에는 특이하게 동해에서 강풍의 출현 확률이 가장 높게 나타난다. 이것은 이 시기에 서해를 통과하여 동쪽으로 이동하는 온대저기압이 동해에서 폭발적으로 발달하는 경우가 많기 때문으로 사료된다(Oh et al, 2015).
5. 요약 및 결론
해상풍은 파랑과 해일 등 해양에서 발생하는 위험기상을 예측하거나 해상의 풍력자원 및 극값 추정을 위해 필수적인 자료이다. 그러나 해상은 육상과는 달리 관측지점이 매우 적고, 위성기반 해상풍도 그 특성상 시공간적으로 연속적으로 자료를 얻는 데 제한이 있다. 또한 널리 사용되는 Holland 경험모델 자료도 태풍의 외곽 바람을 모의하지 못하고 비 태풍 시기에 풍속을 추정하지 못한다. 본 연구에서는 이러한 한계를 극복하기 위하여 태풍 보거싱과 중심위치보정 기법이 사용되어 태풍 시기 강한 바람의 정확도가 높아진 미국 국립환경예보센터의 GFS 재분석 바람장(6시간 간격, 0.5° x 0.5° 공간해상도, 총 기간 10년)을 이용하여 한반도 근해에서 재현빈도별 극치풍속을 추정하였다.
먼저 한반도 근해의 17개의 해양기상 부이를 이용하여 사용된 GFS 재분석 바람장의 정확도를 조사하였다. 그 결과, 자료기간 동안 Bias는 -0.33m/s, RMSE는 1.95m/s, 상관도는 0.86으로 나타나, GFS 바람장이 한반도 근해의 해상풍을 비교적 정확하게 모의하는 것으로 나타났다. 태풍 시기의 강한 바람을 따로 분석해 보아도, 그 오차가 일반적인 재분석 바람장에서 나타나는 과소모의 현상이 나타나지 않아 GFS 분석장이 태풍 시기의 강한 바람도 현실적으로 잘 모의하고 있음을 알 수 있다. 특히, 2018년 19호 태풍 솔릭의 경우, 크기가 작아 해상도가 낮은 바람 자료에서는 태풍 눈벽 주변의 강한 바람이 모델에서는 잘 모의되기 어려운 상황임에도, GFS 바람장은 한반도 근해 부이에서 관측되는 최대 풍속을 비교적 정확하게 모의하였다. 이것은 GFS 재분석에 사용된 태풍 보거싱과 중심위치보정 기법이 외해뿐 아니라 태풍 변형이 심한 근해 및 연안에서도 잘 적용되고 있음을 나타낸다.
GFS 재분석장의 해상풍이 한반도 근해에서 높은 정확도를 보였지만 자료의 기간(10년)이 짧아 극치분석에는 한계가 있다. 본 연구에서는 이러한 한계를 극복하기 위하여 특정 임계값 이상의 풍속을 모두 사용하여 자료의 개수를 늘이는 Peak-Over-Threshold(POT) 방법과 일반화된 파레토 분포(GPD) 방법을 사용하여 극치분석을 실시하였다. GPD 모델의 임계값은 선행연구를 기반으로 Generalized Extreme Value(GEV) 모델과 GPD 모델의 풍속 차이가 최소가 되는 점으로 정하였다.
본 연구에서는 이러한 방법으로 한반도 근해의 모든 격자점에서 재현기간 50년의 극치풍속을 구하고, 이를 서해, 동해, 그리고 제주도 남부해역으로 나누어 분석하였다. 그 결과, 추정된 극치풍속의 공간적인 분포가 자료 기간 동안 태풍 시기에 나타난 최대풍속 분포와 유사한 형태를 보였다. 이것은 우리나라 근해에서 극치풍속의 공간 분포가 태풍에 의해 크게 영향을 받음을 시사한다. 한편, 임계값(14.77m/s) 이상의 강풍 출현확률을 살펴보면, 모든 해역에서 겨울철에 가장 높게 나타났다. 이것은 여름철 태풍 시기 뿐만 아니라 평균적으로 강한 바람이 자주 출현하는 겨울철의 바람도 우리나라 근해의 해상풍 극치분석에 매우 중요한 역할을 함을 시사한다. 따라서 여름철 태풍 중심 부근의 강한 바람만을 고려하는 Holland 경험모델 또는 유사한 태풍 볼텍스(Vortex) 모델을 이용하여 한반도 근해의 극치풍속을 추정하는 것은 그 정확도에 있어 한계가 있다.
본 연구에서는 비 태풍 시기뿐 아니라 태풍 시기의 강한 바람에 대해 정확도가 높은 해상풍 자료를 확보하여 한반도 근해의 극치풍속을 추정하였다. 이 결과는 해상풍력단지의 건설을 포함한 다양한 해상구조물 설계를 위한 기초자료로 사용될 수 있을 것이다. 향후에는, 본 연구를 더욱 발전시켜, 장기간의 자료가 존재하는 재분석 바람장에 태풍 볼텍스 모델을 결합시켜 태풍 바람이 잘 모의된 장기간의 해상풍 자료를 생산하고, 이를 극치풍속 추정에 이용하고자 한다.







 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print